Macro Investing 3: the Principle of Compound Interest
October 8, 2006
Probably everyone is aware of the example of compound interest, which goes something like this. If you start with $1,000, and receive interest of 10% annually, after twenty years, you will have a respectable $6,727.50. And after forty years, you will have a phenomenal $45,259.30! Wow! Now we can all get rich!
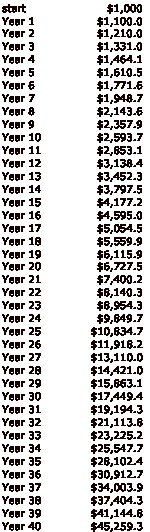
Of course, we know that this never happens. Otherwise the Romans or the Egyptians would own everything. Just try compounding for 2,000 years.
Why doesn’t this work as advertised? Let’s look at some basic problems. First and foremost: you can’t get paid 10% interest on a risk-free asset. For assets with credit risk, on average, the amount that they return over a risk-free rate will be equivalent to credit losses (default, bankruptcy, etc) and other impairment associated with owning this sort of asset. Thus, to take an example from today, if you take only a so-called (ha ha) “risk free rate,” namely the rate on 10-year US Treasury Bonds, about 4.60% today, the situation is not quite so exciting.
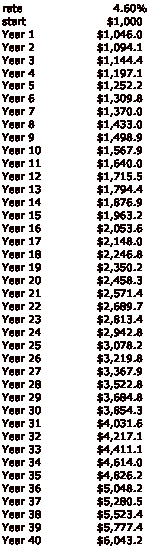
Wow, major letdown. Now our fabulous $45,000 retirement account has been whittled down to $6,043.20. Still, not the worst thing ever, right?
Now, let’s add taxes. At a typical 35% marginal tax rate for interest income, your 4.60% risk-free rate crumples down to 2.99%. And your retirement account?
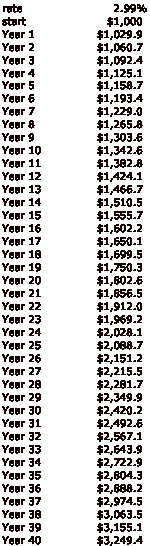
Down to a mere $3,249.40. Now, that is not bad. Actually, starting with $1,000 and ending with more than $1,000, after all the vagaries of history over forty years, is not a terrible outcome. However, that is not the kind of whopper payout that inspires people to undertake a 40-year savings program, certainly not when you must start at a young age, with all the other distractions for uses for your money.
But what about the purchasing power of your money, forty years from now, compared to today. If it takes $4 to buy, forty years from now, what it takes $1 to buy today, then we can see that we are barely keeping even. The “risk free rate” is not risk free. There is the ever-present risk of inflation and currency devaluation. Or, sometimes, currencies just disappear altogether. What if your savings account was in Brazilian cruzeros, German Reichmarks, Italian lira, or Russian roubles? You’d get a big fat zero at the end of the day, or nearly so, no matter how many years of compounding you had accumulated up to that point.
Ah, you say, let’s stick to gold-pegged currencies only! Good idea. Because gold is the ultimate historical currency, and has never been “devalued.” If you had invested in British Pound bonds in 1750, you wouldn’t have suffered any permanent devaluation in the hundred years to 1850. However, you would have only gotten paid about 2.7% per annum for your trouble. Let’s round up a bit to 3.00% — but of course we will take off today’s 35% taxes on interest income, giving us an effective rate of 1.95%
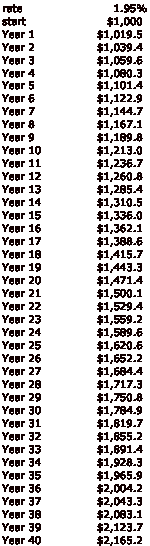
How not-exciting. Still, having $2,165.20 at the end of the exercise, in gold-linked currency, is not bad. If you had instead bought $1,000 of gold bullion at the start, you would end up with $1,000 of gold bullion. So, this is twice as good, over the course of forty years. But what if, at some point during those forty years, the currency that you assumed would remain gold-linked until the end of time was instead devalued, as the British Pound was in 1931? Well, then you might end up with the equivalent of $1,000 gold after forty years, or maybe less. And if the bank that holds your CDs goes bust, or a civil war forces you to leave the country on short notice never to return, or a new government repudiates the debt of the previous government, or a hundred other things that happen to virtually any country if you wait long enough happen, you might end up with zero.
Now we see the reason why this week’s note is entitled “the principle of compound interest.” Because, the fact of the matter is, it is not all that easy, indeed perhaps all-but-impossible, to build significant wealth in the course of a lifetime with a know-nothing, passive compound interest strategy. However, we can see from this example, that if we are able to compound our real, after-tax wealth by a relatively modest 10%, over the course of decades, then we can indeed achieve very nice results. And if we can compound at 20%, we can achieve phenomenal results.
To do this, however, you have to be an active investor. You have to buy those few assets that are cheap and have good prospects, and can thus return in excess of 10% annually, and avoid those assets that are dear or risky, and likely to return less than 10%. This doesn’t mean that you have to trade every day. Maybe you could just buy US stocks or bonds in 1982, and sell in 2000. Then you would have likely made about 12% per year, before taxes. However, if you had instead bought US stocks and bonds in 1965 and sold in 1982, you would have been obliterated by the inflation of that period.
Here’s the next problem. To be an active investor, you need the skills necessary to produce these kinds of returns. You can’t learn them in school, and it is very hard to find an asset manager who can provide them for you. In any case, you will probably have to learn these skills just to be able to identify a manager with these skills, who is in an institutional framework in which he can put them to use. Or, like most of Warren Buffett’s early investors, you have to get real lucky.
It takes many years and typically hard experience to learn these skills, and only a few child prodigies, like Mr. Buffett, can acquire them before age 30. Thus, the notion that someone could start a “compounding program” like this at age 17 is not at all likely, unless they have caring parents who are themselves masters of investing, and, even more unlikely, they share an interest in their parents’ business!
Another corollary of the “principle of compound interest” is that you must avoid losing money. You can go up 20% in one year and up 5% the next, producing an average of about 12% or so. You can even go up 30% in one year and down 5% the next, for an average of about 11%. But you can’t make 10% per year for five years, patting yourself on the back for your success, and then go down 50% in year 6. That’s a road to nowhere. This is complicated, because market prices go up and down, and one is always “losing money” for at least a short period in any investment. Mr. Buffett says that “rule number one of investing is Don’t Lose Money,” and then also says that one should ignore Mr. Market, and be willing to see a decline of as much as 50% in the market price of your asset, due only to typical market fluctuations of no great importance. Isn’t this contradictory? Let us just say that mastery of the principles embodied in Mr. Buffett’s comments doesn’t come easy.
Now we see what we are trying to accomplish with a strategy of macro investing, or indeed any investment strategy: to produce a return significantly greater than any passive strategy, which has the possibility of producing life-changing results within the course of a lifetime. To do this, we need a long-term average, currency-devaluation-adjusted, after-tax return of at least 10%, and better yet 15% or higher. (Most wealthy people in the US don’t get rich by this method. Usually, they own a successful business of some sort. Sometimes they have a high-paid job and manage to save a large portion of their income. Others inherit it. Occasionally, if they are politicians, judges, police chiefs or the like, they get it by stealing, kickbacks, or bribery.)
It is foolishness for any investor to expect returns of this caliber without taking the years of hard study necessary to learn the techniques that produce these kinds of way-above-average results. Indeed, all the evidence shows that to attempt this would likely produce below-average results. Someone needs to be below average, by definition. Thus, for most would-be investors, individual or institutional, it would probably be best to adopt a simple passive strategy, whether 100% debt instruments or a mix of stock and bond investments. Very few people, even those institutional professionals, are able to truly manage and gain the advantages of a passive portfolio that includes stock investments. They will tend to sell and the bottom and buy at the top. Thus, I would tend to emphasize debt instruments in a know-nothing passive portfolio, with the possible exception of equity investments that have a dividend yield equal to or greater than what one is getting from debt instruments. (Sometimes it’s just that obvious.)