We’ve been talking about The Midas Paradox (2015), by Scott Sumner.
July 23, 2017: The Midas Paradox (2015), by Scott Sumner
July 31, 2017: The Midas Paradox #2: Blame Gold
The primary claim of the book is that gold’s value soared higher, in an unprecedented and disastrous fashion, sometime beginning around 1929.
Over the years, there have been a number of arguments that gold’s value goes up and down by substantial amounts. Other people have said that gold’s value is basically stable, and doesn’t go up and down that much — not enough to matter very much in terms of overall economic performance.
Unfortunately, there is no definitive measure to resolve this debate. There is no perfect scientific standard of monetary value, to which we can definitively compare gold, and thus measure, in a scientific sort of way, variation in gold’s market value. Over the centuries, it has been concluded, based on experience, that gold’s variation in value from this perfect ideal is minor enough that gold itself can be used as a proxy of stable monetary value.
The arguments typically revolve around commodity prices. Today’s Consumer Price Index, and other broad measures of “prices,” compiled by large offices full of government statisticians, basically date from around 1940. People have tried to extend the “CPI” backward in time. During the 1920s and 1930s, this meant using the Bureau of Labor Research Wholesale Price Index, whose behavior is close to a raw commodities index. The point is, “prices” before 1940 or so mostly mean what we would today call commodity prices, which is very different in behavior from today’s CPI.
Commodity prices go up and down, compared to gold. This could be a reflection of the supply and demand for commodities. A surplus of wheat or a shortage of copper. Or, it could represent some variation in the value of gold.
This debate has been around a long time. David Ricardo mentioned that it was common during the debates of the 1800-1815 period, when the British Parliament was talking about returning to a gold standard system after a long period of a floating pound that began in 1797. Typically, the debate has broken into two camps:
Camp 1: People who assume that the “value” of gold is the same, identical, defined as: the “purchasing power” of gold compared to some price index, typically a commodity price index. These people don’t even take up the question at all, they simply avoid it from first principles. Obviously, this assumes that the “value” of a commodity index, or whatever price index is used, is, by definition, a measure of perfectly stable value, rather than something whose value might go up and down due to the supply/demand characteristics of commodities; or, on a broader basis the “aggregate supply/aggregate demand” of the economy as a whole, which is a roundabout way of saying that commodity prices (or whatever prices you are using) could go up or down because of overall economic issues not related to monetary value. Once you have made that assumption, then the natural conclusion is that gold’s value goes up and down quite a lot, and is wholly responsible for all variation in your price index. These people tend to become commodity basket targeters of one flavor or another, for obvious reasons. They have been around at least since Irving Fischer’s arguments around 1911.
The contemporary analog is those people who assume that the floating fiat dollar, which everyone knows is a floating currency whose value goes up and down in the forex market vs. other floating currencies, is nevertheless a perfectly stable measure of value when compared to gold; and that all variations in the nominal market price of gold represent variations in the value of gold, measured in a perfectly stable measure of value, the floating fiat dollar. The conclusion is, naturally, that “gold is very volatile.” This is, I hope you agree, rather stupid; but these people are everywhere, and holding a PhD in economics does not seem to cure the condition.
Camp 2: People who take up the topic seriously, and try to tease out any evidence of significant changes in gold’s value. These people admit that no ultimate definitive answer exists; and that the value of gold cannot reasonably be considered to be perfectly unchanging in value, like some known constant of physics; but, weighing all that is available, they conclude that the value of gold appears to be pretty stable, and that most of the variation in commodity prices vs. gold is related to changes in the value of commodities, not gold.
April 7, 2017: What Are Our Stable Money Alternatives?
I have been making this distinction myself since Gold: the Once and Future Money (2007), continuing a long tradition among the better Classical economists of the past 200 years.
Changes in the purchasing power of money, i.e., in the exchange ratio between money and the vendible goods and commodities, can originate either from the side of money or from the side of the vendible goods and commodities. The change in the data which provokes them can occur either in the demand for and supply of money or in the demand for and supply of the other goods and services.
Ludwig von Mises, Human Action (1949)
In investigations into the nature of changes in the value of money it is usual to distinguish between two sorts of determinants of the exchange ratio that connects money and other economic goods; those that exercise their effect on the money side of the ratio and those that exercise their effect on the commodity side. This distinction is extremely useful; without it, in fact, all attempts at a solution would have to be dismissed beforehand as hopeless.
Ludwig von Mises, The Theory of Money and Credit (1912)
It has been my endeavor carefully to distinguish between a low value of money and a high value of corn, or any other commodity with which money may be compared. These have been generally considered as meaning the same thing; but it is evident that when corn rises from five to ten shillings a bushel, it may be owing either to a fall in the value of money or to a rise in the value of corn. …
The effects resulting from a high price of corn when produced by the rise in the value of corn, and when caused by a fall in the value of money, are totally different.
David Ricardo, Principles of Political Economy and Taxation (1817)
It has indeed been said that we might judge of [a currency’s] value by its relation, not to one, but to the mass of commodities. …
To suppose that such a test would be of use in practice, arises from a misconception of the difference between price and value. …
Nothing is so easy to ascertain as a variation of price, nothing so difficult as a variation of value; indeed, without an invariable measure of value, and none such exists, it is impossible to ascertain it with any certainty or precision. …
Commodities generally, then, can never become a standard to regulate the quantity and value of money; and although some inconveniences attend the standard which we have adopted, namely, gold and silver, from the variations to which they are subject as commodities, these are trivial, indeed, compared to those which we should have to bear, if we adopted the plan recommended.
David Ricardo, “Proposals for an Economical and Secure Currency,” (1816)
So, as you can see, this has been around a long time. And, I am not making up anything new here.
Now, let’s move forward from 1815 to 2015, and see why Sumner thinks that gold’s value was going up and down (mostly up) in some kind of catastrophic manner:
Because all prices are measured in money, changes in its real value, or purchasing power, are inversely proportional to changes in the overall price level. (p. 25)
If the nominal price of gold is fixed, as under a gold standard, then by definition a higher purchasing power for gold means a lower price level. (p. 25)
Now, the price level will be inversely proportional to the real value of gold, where the term “value” refers to purchasing power. (p. 26)
To develop an explanation for why the real value of gold (i.e., its purchasing power) rose so dramatically during the 1930s, we need to focus on the world gold market. (p. 425)
That is about as clear a statement as you could hope for. Sumner is declaring himself a member of Camp 1 — those who assume/define the “value of money” to be its purchasing power. From this, it immediately follows that any changes in “purchasing power” i.e. prices, are wholly cased by changes in the value of money.
This is not so uncommon actually. We saw that similar thinking rather badly colored other “interpretations” of the Interwar Period.
November 6, 2016: Robert Mundell’s Interpretation of the Interwar Period
November 13, 2016: Robert Mundell’s Interpretation of the Interwar Period 2: the “Mundell-Johnson Hypothesis”
From this, having assumed that all price changes represent changes in the value of money, and since money was linked to gold (the gold standard) and thus changes in the value of gold, we naturally must assume that changes in the value of money were due to changes in the supply/demand for gold.
Sometimes, economists just sort of let these assumptions slip out without really being aware that the hold them. Sumner, however, pretty much lays it on the table.
He even turns it into a mathematical equation — as if this relationship was enshrined in physical law, like E=Mc^2. (page 27)
Price Level = (gold supply)/(real gold demand)
Obviously, this excludes any influence on Prices besides changes in the value of gold. Basically, this is a deconstruction. The first assumption is:
Price Level = 1/Value of Gold
Sumner says: “the price level will be inversely proportional to the real value of gold, where the term ‘value’ refers to purchasing power.” (p. 26).
Now, we seem to separate the Value of Gold into Supply and Demand:
value of gold = (real gold demand)/(gold supply)
Now, this might seem pretty reasonable at one level. We are just representing here that gold’s value is the balance of supply and demand. Right?
No.
(gold supply) is defined as: “the nominal monetary gold stock.” (p. 27) This does not include all gold, since most gold then and now was “nonmonetary.” Nevertheless, it is simple enough. Since gold coins were relatively unusual by 1930, this is almost entirely central bank gold holdings, which we know.
I could not find a direct mention of the definition of (real gold demand) in the Introduction. But, based on what we have seen (on p. 26) I am pretty sure that it represents what “real” statistics mean throughout economic terminology, which is:
(nominal value)/(price level)
Thus, the (real gold demand) means:
(monetary gold stock)/(price level)
What does this mean? It means that, as the price level falls, but monetary gold remains unchanged, the “real gold demand” also increases. Usually, when we say “demand,” we mean someone actually acquiring something. But here, “real gold demand” can go up even if nobody acquires anything. (real gold demand) can even go up when the monetary gold stock declines, if prices are declining faster. In other words, selling = buying. This is not what people generally mean by “demand” at all.
From this, we can see that:
Price Level = (gold supply)/(gold supply/price level)
If you have a daughter taking Algebra I, she can probably tell you that this is the same as:
Price Level = Price Level
But, since we have already established that:
Price Level = 1/Value of Gold
This naturally follows.
Sumner then divides (real gold demand) further, by breaking it down into (gold reserve ratio)*(real money demand). The (gold reserve ratio) is (gold reserves/monetary base). (real money demand) is: (monetary base)/(price level).
This doesn’t really accomplish much mathematically. Mathematically, we have:
Price Level = (gold supply)/((gold supply/monetary base)*(monetary base/price level))
or:
Price Level = Price Level
But, it does allow the introduction of some new ideas. Demand for monetary gold is related to the demand for base money, times some reserve ratio. Now we can start blaming central banks for changing reserve ratios, and also blaming the public at large for demanding more base money.
From here, you can express changes in terms of the “difference of logs”, which is a somewhat complicated way of saying, percentage changes (it is not quite the same, but close). Thus:
Price Level Change % = (gold supply change %)+(real gold demand change %)
Following our earlier arguments,
(real gold demand change %) = (reserve ratio change %)+(real money demand change %)
This leads to tables such as this one:
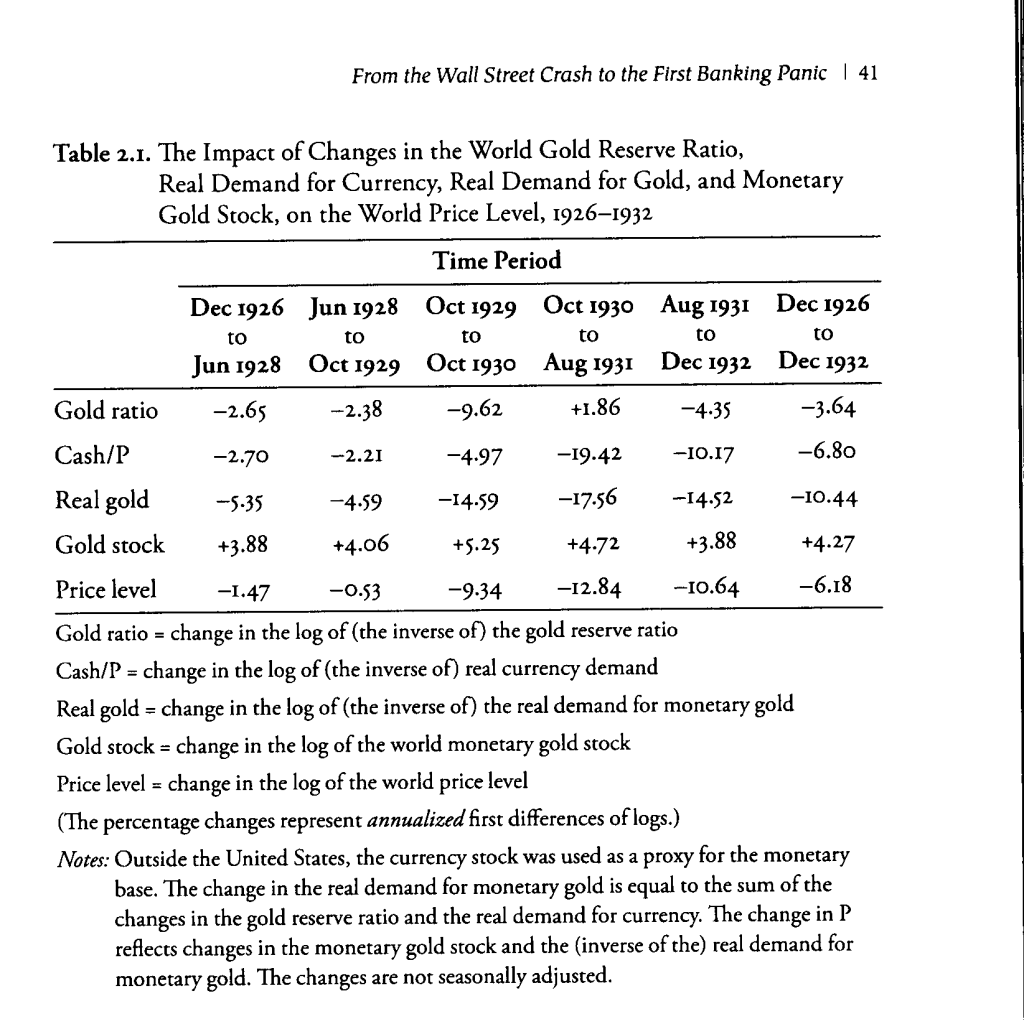
Basically, this says that, from 1926 to 1932, the price level fell at an annualized -6.18% rate; and this fall “could be explained” as an “increase in real gold demand” accounting for -10.44%, against an “increase in supply [gold stock]” of +4.27%. The “increase in real gold demand” can be further separated into an “increase in the gold reserve ratio” accounting for -3.64%, and an “increase in real monetary demand” accounting for -6.80%.
Despite the seeming precision of decimal places, none of this is based on anything in the real world. The only things that were actually measured were the nominal monetary gold stock, the price level, and the monetary base. Everything else is derived from the assumption/definition of (1/value of gold)=(price level), plus some subdivision of those terms. Whatever the nominal monetary gold stock, and whatever the monetary base might have been — it could be anything — some sort of “influence” on the price level would have been assigned anyway.
Sumner then defines what he calls “private gold hoarding.” It is:
“If we focus on monetary gold stocks, then flows in and out of private gold hoards show up as changes in the supply of monetary gold. This is a bit awkward since one normally thinks of the term ‘private gold hoarding’ as applying to the demand for gold. There are several reasons, however, why it makes more sense to model the supply of monetary gold, rather than the total gold stock. First, we have relatively good monthly data on monetary gold stocks, particularly during the late 1920s and early 1930s. More importantly, it simplifies the process of modeling the key determinants of the price level.” (p. 28)
What does this mean?
It means that any increase in the gold holdings of central banks (monetary gold) is now “central bank gold hoarding,” especially if it is related to an increase in the gold reserve ratio. That’s bad. That’s deflationary.
Also, it means that any decrease in the gold holdings of central banks is now “private gold hoarding.” That’s also bad, and also deflationary.
We know it was “deflationary,” because we already defined any decline in the price level as being due to an increase in the value of gold; and since this increase in the value of gold must come about by “demand,” we can then call it “hoarding,” because prices went down.
Riiiiiight.
At other times — when “prices” were rising, we can use the inverse. A decline in central bank holdings is “dishoarding by central banks.” An increase in central bank holdings is “private market dishoarding.” We know it was “dishoarding,” not “hoarding,” because prices went up.
By now, you should be getting the sense that all of this is a big airball. There’s really nothing here except the original assertion that price level = (1/value of gold), which is itself a big airball. Now, the basic premise that the value of gold might have changed by some catastrophic degree, and this might be reflected in some kind of statistic that we can see and evaluate and come to a conclusion about, is not a bad one. We can allow that possibility, even though there is no other such example in half a millennium that I am aware of. But, there is no such investigation here, in all of these hundreds of pages. There is no need for one. We assumed it away at the beginning.
From this, you can then extend to what appears to be a very precise look into the effects of “changes in the value of gold” upon the “price level.” Every little wiggle in the price level can be “explained” by definition, as some sort of change in the “value of gold.” And, every tiny wiggle in monetary gold — whether up or down! — can be described as “central bank hoarding,” “private market hoarding,” “central bank dishoarding,” or “private market dishoarding,” depending on what your narrative requires. We can do this because we have already determined that price level = (1/value of gold), so it doesn’t really matter what the “evidence” is, because we don’t need it. We already came to our conclusion on page 26. The “evidence” is just some window dressing for giggles.
Next week, we will look at some real evidence, that we can see and evaluate and come to a conclusion about. I have to do this because Sumner does not. The evidence we will look at is not in this book.